팁 1 : 숫자를 이진 표기법으로 변환하는 방법
팁 1 : 숫자를 이진 표기법으로 변환하는 방법
일반적인 십진법 이외에 미적분학, 다른 시스템이 있습니다. 가장 일반적인 것은 2 진수, 8 진수, 16 진수입니다. 이 시스템은 주로 컴퓨터 기술에 사용됩니다. 하나의 시스템에서 숫자를 번역하려면 미적분학 다른 하나에는 간단한 조작이 있습니다. 번역하는 방법을 고려하십시오. ~의 수 바이너리로 시스템 미적분학 다른 시스템에서.

지침
1
8 진수를 번역하려면 ~의 수 바이너리로 시스템 양식에 각 그림을 제시해야합니다.3 진수의 2 진수. 예를 들어, 8 진수 765는 다음과 같이 triads로 분해됩니다. 7 = 111, 6 = 110, 5 = 101 결과는 2 진수 111110101입니다.
2
16 진수를 번역하려면 ~의 수 바이너리로 시스템 미적분학 양식에 각 그림을 제시해야합니다.2 진수 십진수 예를 들어, 16 진수 967은 다음과 같이 tetrads로 분해됩니다. 9 = 1001, 6 = 0110, 7 = 0111 결과는 100101100111의 2 진수입니다.
3
10 진수를 2 진수로 변환하려면 시스템 미적분학, 결과를 전체적으로 작성할 때마다 항상 두 개로 나눌 필요가 있습니다 ~의 수 나머지는 분열은 하나의 숫자가 될 때까지 계속되어야합니다. 최종 수는 최종 분할의 결과와 모든 분할의 나머지를 역순으로 순차적으로 기록하여 얻습니다. 예를 들어, 그림은 십진수를 변환하는 절차를 보여줍니다 ~의 수 25에서 2 진수로 시스템 미적분학. 연속적인 2로 나누면 다음과 같은 잔차가 생깁니다 : 10011. 반대로 확대하면 필요한 수를 얻습니다.

팁 2 : 이진으로 변환하는 방법
전자 기계의 구성 요소또한 컴퓨터가 있으며 두 가지 구별 가능한 상태가 있습니다. 전류가 있고 전류가 없습니다. 그들은 각각 "1"및 "0"으로 지정됩니다. 그러한 상태가 두 가지 밖에 없으므로 전자 기기의 많은 프로세스와 연산은 이진수를 사용하여 설명 될 수 있습니다.

지침
1
분수 십진수를 번역하려면숫자를 이진수 시스템에서 계산하려면 다음 알고리즘을 따르십시오. 235.62의 예제를 사용하여 알고리즘의 연산을 고려하십시오. 먼저 숫자의 정수 부분이 변환됩니다.
2
10 진수를 2로 나눌 때까지우리는 불가분의 잔류 물을 얻는다. 각 분할 단계에서 나머지는 1 (배당 수가 홀수 인 경우) 또는 0 (배수가 나머지없이 2로 나눌 수있는 경우)입니다. 이 모든 잔류 물을 고려해야합니다. 이러한 단계별 나누기의 결과로 얻은 마지막 부분 결과는 항상 하나의 단위가 될 것이고, 마지막 단위를 필요한 2 진수의 최상위 자릿수에 쓰고 그 과정에서 얻은 나머지를 역순으로이 단위에 기록합니다. 여기서주의해야하며 0을 건너 뛰지 마십시오. 따라서 바이너리 코드에서 235의 숫자는 11101011의 숫자와 일치합니다.

3
이제 이진수 시스템으로 변환하십시오.십진수의 소수 부분. 이를 위해 숫자의 분수 부분에 2를 곱하고 얻은 숫자의 정수 부분을 수정합니다. 이러한 정수 부분은 직 접 순서에서 이진 지점 다음의 이전 단계에서 얻은 번호에 더해진다. 그런 다음 소수 부분 수 235.62는 이진 부분 11101011.100111에 해당한다.

팁 3 : 번호 시스템을 번역하는 방법
정보 기술에서 일반적인 십진수 시스템 대신 컴퓨터의 작업이 이뤄지면서 종종 바이너리가 사용됩니다.

지침
1
주요 작업은 두 가지입니다. 십진수에서 다른 십진수 (2 진수, 8 진수 등)로 변환하거나 그 반대로도 가능합니다. 각 숫자 시스템의 이름은 그 기본 요소 (2 진수 - 2, 10 진수 - 10)의 요소 수입니다. 베이스가 10보다 큰 기본 표기법 시스템에서는 두 자리 숫자를 대신하여 라틴 알파벳 (A-10, B-11 등)의 문자를 사용하는 것이 일반적입니다.
2
바이너리 시스템의 예제를 사용한 연산을 생각해 봅시다.번호 매김. 다른 모든 시스템의 경우 기본 2를 해당하는 것으로 대체하는 것과 동일한 규칙과 방법이 적용되므로 몇 자리 숫자로 구성된 이진수 시스템에 숫자가 있습니다. 우리는 숫자에 2를 곱한 값의 합으로 이것을 씁니다. 다음으로 우리는 모든 힘을 0에서 시작하여 오른쪽에서 왼쪽으로 정렬합니다. 우리는 요약합니다. 결과 숫자는 찾고자하는 숫자입니다. 예 1011 = 2 * 2 + 11.
3
이제 역 동작을 고려하십시오.십진법에 숫자가 주어 지도록하십시오. 우리는 그것을 우리가 번역하고자하는 숫자 체계에 기초하여 칼럼으로 나눌 것입니다 (우리의 경우는 2가 될 것입니다). 개인은 땅보다 적게 될 때까지 부서는 끝까지 계속됩니다. 다음으로, 마지막부터 시작하여 줄의 모든 유적을 적어 둡니다. 예 11/2 = 5 나머지는 1, 5/2 = 2, 나머지는 1, 2/2 = 1 나머지는 0 => 1011입니다. 다른 예는 그림과 같습니다. 라틴 문자로 해당 숫자 체계에서 10으로 시작하는 숫자를 대체하는 것을 잊지 마십시오! 그렇지 않으면 "10"과 "1" "0"은 완전히 다른 것들이므로 결과 숫자가 잘못 읽힐 것입니다! 숫자가 표현되는 숫자 시스템의 밑줄은 숫자의 가장 오른쪽 숫자의 맨 아래에 색인 형태로 표시됩니다.
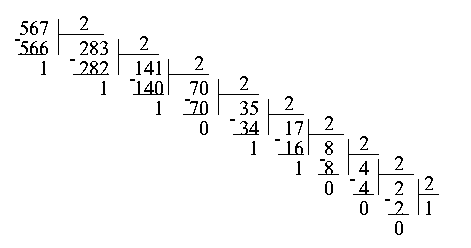
팁 4 : 한 시스템에서 다른 시스템으로 숫자를 변환하는 방법
우리가 사용하는 계정 시스템에서하루 10 인물 - 0에서 9. 따라서이를 십진수라고합니다. 그러나 기술적 인 계산, 특히 컴퓨터와 관련된 계산에서는 시스템, 특히 2 진수와 16 진수. 번역 할 수 있어야합니다. ~의 수 한 명으로부터 시스템 다른 번호 매기기.

너는 필요할거야.
- - 종이 조각.
- - 연필 또는 펜;
- - 계산기.
지침
1
이진 시스템이 가장 간단합니다. 0과 1의 두 자리 만 있습니다. 이진수의 각 자릿수 ~의 수끝에서부터 시작하여 2의 거듭 제곱에 해당합니다. 2도에서 0도까지는 1과 같고, 1 - 2, 2 - 4, 3 - 8 등입니다.
2
이진수가 1010110이라고 가정합니다. 그것에있는 유닛은 들판의 끝에서 두 번째, 세 번째, 다섯 번째 및 일곱 번째에 서 있습니다. 따라서 십진법에서이 수는 2 ^ 1 + 2 ^ 2 + 2 ^ 4 + 2 ^ 6 = 2 + 4 + 16 + 64 = 86과 같습니다.
3
역의 문제는 십진수의 변환입니다. ~의 수 이진 시스템에서. 바이너리 레코드를 얻으려면이 숫자를 순차적으로 2로 나누고 나누기의 나머지 부분을 써야합니다. 첫 번째 단계는 마지막 숫자 57/2 = 28 (균형 1)을 제공합니다. 그러면 28/2 = 14 (나머지 0) 다음 단계는 다음과 같습니다. 14/2 = 7 (나머지 0), 7/2 = 3 (잔액 1), 3/2 = 1 (잔액 1), 1/2 = 0 (잔액 1)로 나눌 수 있습니다. 111001 = 2 ^ 0 + 2 ^ 3 + 2 ^ 4 + 2 ^ 5 = 1 + 8 + 16 + 32 = 57 : 정답을 확인하십시오.
4
에서 사용 된 두 번째 숫자 시스템컴퓨터 문제 - 16 진수. 10 개가 아니라 16 개 숫자입니다. 새 기호를 만들지 않으려면 16 진수의 처음 10 자리 시스템 보통 자릿수로 표시되며, 남은 여섯 개는 라틴 문자로 표시됩니다. A, B, C, D, E, F 십진수 표기법 ~의 수m을 10에서 15로 변경하십시오. 혼란을 피하기 위해 # 또는 0x 문자 앞에는 16 진수 시스템으로 작성된 숫자가옵니다.
5
숫자를 16 진수로 변환하려면 시스템 10 진수로, 당신은 각각의 수를16의 해당 학위와 결과를 추가합니다. 예를 들어 10 진수 표기 # 11A는 10 * (16 ^ 0) + 1 * (16 ^ 1) + 1 * (16 ^ 2) = 10 + 16 + 256 = 282입니다.
6
십진수에서 역 변환 시스템 16 진법은 같은 방법으로 행해진 다.잔류 물은 2 진수와 같다. 예를 들어 10,000이라는 숫자를 16으로 나누고 나머지를 녹음하면 10000/16 = 625 (balance 0) .625 / 16 = 39 (balance 1) .39 / 16 = 2 (balance 7) .2 / # 2710 = 1 * (16 ^ 1) + 7 * (16 ^ 2) + 2 * (16 ^ 3) = 16 + 1792 계산의 결과는 16 진수 # 2710입니다. + 8192 = 10000이다.
7
번역 ~의 수 16 진수에서 시스템 이진수의 번호 매기기는 훨씬 간단합니다. 숫자 16은 2의 제곱입니다 : 16 = 2 ^ 4. 따라서 각 16 진수는 4 자리 2 진수로 쓸 수 있습니다. 이진수에 4 자 미만인 경우 처음에 0을 추가하십시오 (예 : # 1F7E = (0001) (1111) (0111) (1110) = 1111101111110). ~의 수 십진수 표기법은 8062입니다.
8
역 변환의 경우, 바이너리를 분할해야합니다.끝부터 네 개의 숫자 그룹의 수, 각각의 이러한 그룹은 16 진수 # 31A9을 준다 (0011)로 변환 진수 tsifroy.Naprimer, 11,000,110,101,001 (0001) (1010) (1001), 대체. 10 진법으로 확인 응답 전송의 정확성 : 모두 ~의 수 12713과 같습니다.
팁 5 : 숫자를 이진수로 변환하는 방법
제한된 심볼 사용으로 인해 이진 시스템은 컴퓨터 및 기타 디지털 장치에서 사용하기에 가장 편리합니다. 기호는 2 : 1과 0이므로 시스템 등록 기관 업무에 적용된다.

지침
1
이진 시스템은 위치 적이다.즉. 숫자에서 각 숫자의 위치는 해당 숫자에서 2와 같은 특정 숫자에 해당합니다. 학위는 0에서 시작하여 오른쪽에서 왼쪽으로 이동할 때 증가합니다. 예를 들어, ~의 수 101은 1 * 2 ^ 0 + 0 * 2 ^ 1 + 1 * 2 ^ 2 = 5와 같습니다.
2
번역하기 ~의 수 다른 번호 시스템에서 바이너리로,두 가지 방법을 사용할 수 있습니다 : 2로 나누는 연속적인 나누기 또는 테이블의 숫자의 각 숫자를 해당하는 4 진수의 4 진수로 변환합니다.
3
위치 시스템 간의 광범위한 분배또한 8 진수, 16 진수 및 10 진수 시스템을 사용하십시오. 그리고 첫 번째 두 번째 방법이 더 적용 가능하면 둘 다 십진법에서의 변환에 적용 할 수 있습니다.
4
10 진수를 2 진수로 변환하는 것을 고려하십시오. 시스템 2로 연속 나누기의 방법으로. 십진수를 번역하려면 ~의 수 25 바이너리 코드로, 당신은 2로 나눌 필요가각 분할 단계에서 얻어진 잔차는 오른쪽에서 왼쪽으로 행에 기록되고, 마지막 나머지의 숫자를 기록한 후 최종 2 진수가됩니다 ~의 수. 나머지는 => 1; 12/2 = 6, 나머지는 존재하지 않음 => 0, 6/2 = 3, 나머지는 존재하지 않음 => 0, 3/2 = 1, 나머지 => 1, 1; = 0, 나머지 1 = 1입니다. 변환의 레코드는 다음과 같습니다. 25_10 = 11001_2.
5
8 진수 및 16 진수바이너리 시스템의 네 개의 코드 심볼에 대응하는 각 자리를 바꾸어 진 코드로 번역된다. 다음과 같이 변환 테이블이 = 0000 = 0001 1 0 3 = 0011 = 0010 2, 4 = 0100 = 5 0101 6 0110 7 = 0111 = 8 = 1000 = 1001 9, A = 1010 B = 1011, C = 1100, D = 1101, E = 1110, F = 1111.Naprimer : 61_8 => [6 = 0110] [0001 = 1] => 01100001_2; 9EF_16 => [= 1,001 9] E = 1110] [F = 1,111] => 100111101111_2.
팁 6 : 숫자 시스템이란 무엇입니까?
숫자 체계는 숫자를 쓰는 방법입니다.특수 기호, 즉 서면으로 숫자를 나타내는 데 도움을줍니다. 번호 시스템은 번호에 특정 표준 표현을 제공합니다. 시대와 응용 분야에 따라 다수의 시스템이 존재하고 계속 존재하고 있습니다.

지침
1
기존 번호 시스템은 위치, 혼합 및 비 위치의 세 가지 주요 유형으로 나눌 수 있습니다.
2
위치 확인 시스템에서 부호 또는 번호위치에 따라 다른 값을 가질 수 있습니다. 시스템은 사용 된 기호의 수에 의해 결정됩니다. 가장 널리 사용되고 널리 사용되는 10 진수 시스템. 여기에서 모든 숫자는 0에서 9까지의 10 자리 숫자의 명확한 시퀀스로 표시됩니다.
3
모든 디지털 기술의 작업은 2 진수 시스템을 기반으로합니다. 두 개의 문자 (1과 0) 만 사용합니다. 모든 거대한 숫자는이 숫자의 다른 조합으로 표시됩니다.
4
특정 계산에서 삼항 항 및8 진수 시스템. 알려진 것은 수십 또는 십진법에 의한 소위 카운트라고도합니다. 컴퓨터 과학 및 프로그래밍에서 16 진수 표기법은 매우 인기가 있습니다. 프로그래밍 할 때 데이터 단위 인 기계어를 작성할 수 있기 때문입니다.
5
혼합 숫자 시스템은 위치 시스템과 유사합니다. 혼합 시스템에서는 숫자가 증가하는 순서로 표시됩니다. 이 시퀀스의 멤버 간의 관계는 완전히 다를 수 있습니다.
6
그래서, 넘버링의 혼합 시스템은(1 + 1), 3 (1 + 2), 5 (2 + 1), 2 (1 + 1), 2 3) 등등.
7
형식으로 시간 기록을 나타낼 경우일 -시 - 분 - 초, 그리고 이것은 혼합 숫자 체계이기도합니다. 시퀀스의 모든 용어는 최소, 즉 초 단위로 표현 될 수 있습니다. 수학에서 혼합 시스템의 빈번하게 사용되는 예는 일련의 계승으로 나타나는 계승 번호 시스템입니다.
8
비 위치 시스템에서,시스템의 기호는 고정되어 있으며 위치에 의존하지 않습니다. 이 시스템은 극히 드문 경우이며 수학적으로도 복잡합니다. 그러한 시스템의 전형적인 예는 : Stern-Brocko 수 시스템, 잔류 클래스 시스템, 이항 수 시스템.
9
다른 시간에 다른 민족이 사용했습니다.번호 시스템의 집합. 예를 들어, 오늘날까지 알려진 로마 숫자 체계는 매우 인기가있었습니다. 숫자를 쓰는 데는 라틴 문자 V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000이 사용되었습니다.
10
또한 단일, 이진, 바빌로니아, 히브리어, 알파벳, 고대 이집트, 마야, 키푸, 잉카 등과 같은 번호 체계가 알려져 있습니다.







