팁 1 : 오른쪽 육각형 측면을 찾는 방법
팁 1 : 오른쪽 육각형 측면을 찾는 방법
육각형 - "육각형"- 형태가 있고,예 : 너트와 연필, 벌집 및 눈송이 섹션. 이 형식의 올바른 기하학적 인물은 다른 평면 폴리곤과 구별되는 특정 기능을 가지고 있습니다. 이것은 헥스에 대해 외접하는 원의 반경이 측면의 길이와 동일하다는 사실로 이루어져 있습니다. 많은 경우 다각형의 매개 변수 계산을 크게 단순화합니다.

지침
1
문제의 조건에서, 정확한 거리 근처에 기술 된 반지름 (R) 육각형 계산할 것이 없습니다 -이 값은 육각형의 변의 길이 (t)와 동일합니다 : t = R. 알려진 조광기 (D)의 경우 간단히 반으로 나누십시오 (t = D / 2).
2
정확한 둘레 (P) 육각형 간단한 나누기 연산으로 변의 길이 (t)를 계산할 수 있습니다. 약수로,면 수를 사용하십시오. 6 : t = P / 6.
3
이러한 다각형에 새겨진 반경 (r)원은 측면 (t)의 길이에 약간 더 복잡한 계수 (반경의 두 배)로 연결되고 그 결과를 트리플의 제곱근으로 나눕니다. t = 2 * r / √3. 내접원의 지름 (d)을 사용하는 동일한 공식은 더 많은 수학적 작용이 될 것입니다 : t = d / √3. 예를 들어 반경이 50cm 인 경우 측면 길이 육각형 대략 2 * 50 / √3 ≈ 57,735 cm와 같아야합니다.
4
여섯 개가있는 다각형의 알려진 영역 (S)정점은 그면 (t)의 길이를 계산할 수 있지만, 정확하게 그 관련된 수치 계수 세 정수의 분수로 표현. 세의 제곱근으로 나누어 2/3, 및 제곱근의 값으로부터 얻어진 : t = √ (2 × S / (3 * √3)). 도면의 영역 (400) cm² 출력 인 경우, 예를 들어, 측면 길이가 약되어야 √ (2 × 400 / (3 * √3)) ≈ √ (800 / 5,196) ≈ √153,965 ≈ 12,408cm.
5
오른쪽 주위에 외주 (L) 육각형, 반경, 따라서 측면 길이에 관련됩니다(Pi)의 수로 표현된다. 문제의 조건 하에서 주어진다면, 그 값을 두 개의 수 Pi : t = L / (2 * π)로 나눕니다. 예를 들어이 값이 400cm이면 측면 길이는 약 400 / (2 * 3,142) = 400 / 6,284 ≈ 63,654cm가되어야합니다.
6
내접원에 대해 동일한 매개 변수 (l)를 사용하면 측면의 길이를 계산할 수 있습니다 육각형 그것은 상기 트리플의 제곱근에 의한 PI의 생성물의 비율을 계산하여 (T) : t가 l / = (π * √3). 예를 들어, 내접원 길이가 300cm 인 경우 쪽 육각형 300 / (3,142 * √3) ≈ 300 / (3,142 * 1,732) ≈ 300 / 5,442 ≈ 55,127 cm와 거의 비슷한 값을 가져야합니다.
팁 2 : 육각형의 면적을 찾는 방법
정의에 따르면, 면적 측정은 정확합니다.다각형은 다각형이라 불리며, 변이 서로 같고 각도 동일합니다. 정육각형은 규칙적인 다각형으로, 변의 수가 6입니다. 정다각형의 면적을 계산하기위한 몇 가지 공식이 있습니다.

지침
1
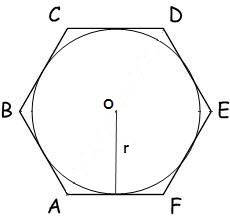
근처에 기술 된 원주의 반지름다각형은 표면적이 식으로부터 계산 될 수있다 : S = (N / 2) • R² N 죄 (2π / N) - • 다각형, R의 양측의 수 - 원의 반경, π = 180º.V 정육각형 모든 각도가 동일 120 °이므로 식의 형식을 가질 것이다 : S = √3 * 3/2 *를 R²

2
반지름이 r 인 원이 새겨 져있는 경우다각형은, 그 영역이 식에 의해 계산된다 : N S = N * R²의 *의 TG (π / N) - 다각형의면의 수는, R - 내접원의 반경, π = 180º.Dlya 육각형, 이것은 수식된다 : S = 2 * √ 3 * R²
3
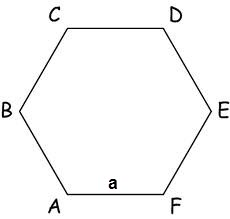
규칙적인 다각형의 영역은 또한화학식의 측면의 길이를 알고 계산 : S = N / 4 * a² * CTG (π / N), N - 다각형의면의 수를 A - 다각형의 측면 길이는 π = 육각형 180º.Sootvetstvenno 지역은 : S = √3 * 3/2 * a²
팁 3 : 실제 단면 값을 찾는 방법
공간에서 인물의 성질은 stereometry와 같은 기하학 섹션에 의해 점유됩니다. 입체 측정법의 문제를 해결하는 주요 방법은 섹션 다면체. 그것은 당신이 올바르게 만들 수있게 해줍니다. 섹션 다면체를 만들고 이들 단면의 형태를 결정할 수 있습니다.

지침
1
정의 섹션 모든 수치, 즉이 자연적 가치 섹션, 경사의 건설에 문제의 공식화에서 수시로 함축된다 섹션. 경사 부분은 더 정확하게 전방 투영 세컨트 평면이라고 부릅니다. 그리고 자연스러운 가치를 형성하기 위해서는 여러 가지 조치를 취하는 것으로 충분합니다.
2
눈금자와 연필을 사용하여3 개의 투영법 - 정면도, 평면도 및 측면도. 주 투영의 정면도에서 경사 투영 선을 그리는 앞 투영 세컨트 평면이 지나가는 경로를 표시합니다.
3
경 사진 선에서 주 요점을 표시하십시오 : 발생 지점 섹션 나가다 섹션. 모양이 직사각형 인 경우 점출입은 한 번에 하나씩이됩니다. 그림이 프리즘이면 점의 수가 두 배가됩니다. 두 점은 모양과 출구로 항목을 정의합니다. 다른 두 개는 프리즘 측면의 점을 결정합니다.
4
임의의 거리에서 직선을 그리고,전방 투영 세컨트 평면에 평행하다. 그런 다음 기본 뷰 축에있는 보조 선을 평행 축과 교차 할 때까지 경사 선에 수직으로 보조 선을 그립니다. 이렇게하면 새 좌표계에서 그림의 투영 된 점을 얻을 수 있습니다.
5
모양의 너비를 결정하려면 직선을 생략하십시오.메인 뷰의 포인트에서부터 상위 뷰까지. 대응하는 지표에 의해 선과 그림의 각 교차점에 대한 점의 투영을 나타냅니다. 예를 들어, 점 A가 그림의 주 형식에 속하면 점 A '와 A "는 투영면에 속합니다.
6
새 좌표계에서 거리를 따로 설정하십시오.주요 지점의 수직 투영 사이에 형성됩니다. 건설 결과로 얻은 수치이며 경사의 자연스런 가치입니다. 섹션.







