팁 1 : 사다리꼴의 기초를 찾는 방법
팁 1 : 사다리꼴의 기초를 찾는 방법
사다리꼴의 밑 부분은 여러 곳에서 찾을 수 있습니다.메소드를 호출합니다. 등변 사다리꼴의 알려진 면적, 높이 및 측면에 대해 계산 순서는 이등변 삼각형의 변을 계산하는 것으로 감소합니다. 또한 이등변 사다리꼴의 특성을 사용하기도합니다.

지침
1
등변 사다리꼴을 그립니다. 사다리꼴의 면적 - S, 사다리꼴의 높이 - h와 측면 - a. 공중 그네의 높이를 더 크게 내립니다. 큰베이스는 세그먼트 m과 n으로 나뉩니다.

2
양쪽베이스 (x, y)의 길이를 결정하려면 등변 사다리꼴의 특성과 사다리꼴의 면적 계산 공식을 적용하십시오.
3
이등변 사다리꼴의 특성에 따르면, 세그먼트 nx와 y의 반의 차이와 같습니다. 결과적으로, 사다리꼴 y의 더 작은 밑변은 더 큰 밑변과 2를 곱한 부분 n의 차이로 표현 될 수 있습니다. y = x - 2 * n.

4
알 수없는 작은 세그먼트 n을 찾으십시오. 이렇게하려면 결과 직각 삼각형의 한면을 계산하십시오. 삼각형은 높이 -h (cathet), 측면 -a (hypotenuse) 및 세그먼트 -n (cathet)에 의해 형성됩니다. 피타고라스의 정리에 따르면, 알려지지 않은 성당 n² = a² - h². 알려진 수치를 대입하고 다리 n의 제곱을 계산하십시오. 결과 값의 제곱근을 취하십시오 - 이것은 세그먼트 n의 길이입니다.

5
이 값을 y를 계산하기위한 첫 번째 방정식으로 대체하십시오. 사다리꼴의 면적은 S = ((x + y) * h) / 2의 공식으로 계산됩니다. 알 수없는 변수를 표현하십시오 : y = 2 * S / h - x.

6
수신 된 두 방정식을 시스템에 기록하십시오. 알려진 값을 대입하여 두 방정식의 시스템에서 두 개의 미지 수량을 찾습니다. 시스템 x의 결과 솔루션은 더 큰 기본의 길이이고, y는 더 작은 기본입니다.

팁 2 : 사다리꼴베이스의 길이를 찾는 방법
이러한 사변형을 사다리꼴로 지정하려면 적어도 세면을 정의해야합니다. 따라서, 예를 들면, 대각선의 길이가 주어진 문제를 고려할 수있다 사다리꼴의, 그리고 측면의 벡터 중 하나.

지침
1
2
ABD 삼각형을 고려하십시오. 그 변 AB의 길이는 벡터 a의 모듈러스와 같습니다. | a | = sqrt ((ax) ^ 2 + (ay) ^ 2) = a라고 가정하면 a의 유도 코사인으로 cosφ = ax / sqrt ((ax) ^ 2 + (ay) ^ 2) 대각선 BD에는 길다 p, 원하는 AD 길다 x. 그런 다음 코사인 정리에 의해 P ^ 2 = a ^ 2 + x ^ 2-2axcosφ. 또는 x2 2axcosφ + (a ^ 2-p ^ 2) = 0.
3
차 방정식의 해법 : X1 = (2acosf + SQRT (4 (a ^ 2) ((사인, 코사인) ^ 2) -4 (a ^ 2-P ^ 2))) / 2 = acosf + SQRT ((a ^ 2) ((사인, 코사인) ^ 2) - (a ^ 2-P ^ 2)) A * 도끼 == | SQRT (((AX) ^ 2 + (AY) ^ 2) + SQRT ((((a) ^ 2) (AX ^ 2)) / (AX ^ 2 + (AY) ^ 2)) - 한 ^ 2 + P ^ 2) = AD.
4
어퍼를 찾으려면 재단 BC (해를 찾기위한 길이를 x라고도 함), 모듈 | a | = a 및 두 번째 대각 BD = q와 각도 (ABC)의 코사인 (분명히 (n-φ)과 동일).
5
삼각형 ABC, k이전처럼 코사인 정리가 적용되고 다음과 같은 해가 발생합니다. AD에 대한 해를 바탕으로 cos (n-φ) = -cosφ를 고려하여, p를 q로 대체하는 다음 공식을 쓸 수 있습니다 : BC = - a * ax | sqrt ((ax) ^ 2 + (ay) ^ 2 ) + sqrt (((a) ^ 2) (ax ^ 2)) / (ax ^ 2 + ay ^ 2)) - a ^ 2 + q ^ 2).
6
이 등식은 정사각형이며,따라서 두 가지 뿌리를 가지고있다. 따라서이 경우 길이가 음수가 될 수 없으므로 양수 값을 가진 루 트만 선택해야합니다.
7
예제 사다리꼴의 AB의 ABCD면은 벡터 a (1, sqrt3), p = 4, q = 6에 의해 주어진다. 찾기 재단 사다리꼴의해상도. 위에서 얻은 알고리즘을 사용하여 | a | = a = 2, cosφ = 1/2로 쓸 수 있습니다. AD = 1/2 + SQRT (4/4 -4 + 16) = 1/2 + SQRT (13) = (SQRT (13) +1) /2.BC=-1/2+sqrt (-3 + 36 ) = (sqrt (33) -1) / 2이다.
팁 3 : 사지의 높이를 찾는 방법
사다리꼴은 사변형이며, y두면은 평행하고 다른 두면은 평행하지 않습니다. 사다리꼴의 높이는 두 개의 평행선 사이에 수직으로 그려지는 선분입니다. 초기 데이터에 따라 다른 방식으로 계산할 수 있습니다.

너는 필요할거야.
- 사다리꼴면의 측면, 밑면, 중간 선뿐만 아니라 선택적으로 그 영역 및 / 또는 둘레에 대한 지식.
지침
1
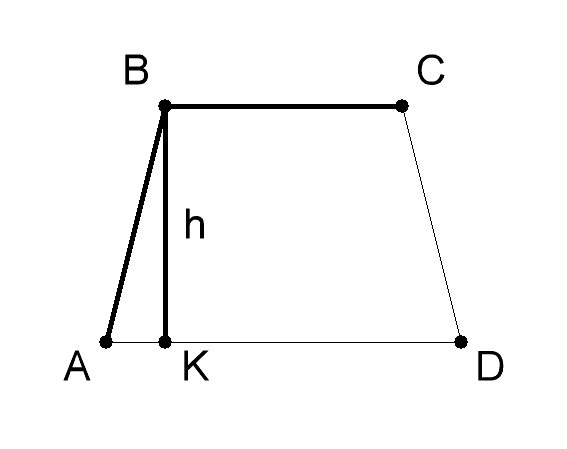
사다리꼴의 면적을 계산하는 한 가지 방법높이와 중심선의 곱입니다. 이등변 삼각형이 있다고 가정하십시오. 그런 다음 밑변 a와 b, 면적 S와 둘레 P를 갖는 이등변 사다리꼴의 높이는 다음과 같이 계산됩니다. h = 2 x S / (P-2 x d). (그림 1 참조)
2
사다리꼴의 면적과 그 기저부 만 알고있는 경우 사다리꼴 면적 공식 S = 1 / 2h x (a + b) : h = 2S / (a + b)에서 높이 계산 공식을 얻을 수 있습니다.
3
동일한 데이터를 갖는 사다리꼴이 있다고 가정합니다.그리고 그림 1에서 우리는 2 개의 높이를 그린다. 두 개의 작은면이 직각 삼각형의 다리 인 직사각형을 얻는다. x에 대해 더 작은 것을 나타냅니다. 그것은 더 큰베이스와 더 작은베이스 사이의 길이의 차이를 나눔으로써 발견됩니다. 그런 다음 피타고라스의 정리에 의해 높이의 제곱은 빗변 d와 X 선의 제곱의 합과 같습니다. 이 합으로부터 근을 추출하여 높이 h를 구합니다. (그림 2)
팁 4 : 직사각형 사다리꼴의 기초를 찾는 법
네 모서리가있는 수학적 수치는 대변의 쌍이 평행이고 다른 한 쌍이 아닌 경우 사다리꼴이라고합니다. 평행면을 호출합니다. 근거 사다리꼴의, 다른 두 - 측면. 직사각형 사다리꼴의 측면 각도 중 하나는 직선입니다.

지침
1
과제 1. BC와 AD 직사각형을 찾아라. 사다리꼴의대각선의 길이 AC = f가 알려져 있다면; 길이옆면 CD = c이고 그것과의 각도 ADC = α 해결책 : 사각 삼각형 CED를 고려하십시오. 알려진 빗변 c와 빗변과 EDC 다리 사이의 각도. CE 및 ED의 변의 길이를 구하십시오. CE = CD * sin (ADC); ED = CD * cos (ADC). 그래서 : CE = c * sinα; ED = c * cosα.
2
직각 삼각형 ACE를 고려하십시오. 사기 AC와 CE는 직각 삼각형의 규칙에 따라 측면 AE를 찾습니다. 다리의 제곱의 합은 빗변의 제곱과 같습니다. 그래서 : AE (2) = AC (2) - CE (2) = f (2) - c * sinα. 방정식의 오른쪽의 제곱근을 계산합니다. 너는 직사각형의 꼭대기 밑을 발견했다. 사다리꼴의.
3
기준 AD의 길이는 2의 길이의 합이다세그먼트 AE 및 ED. AE = 제곱근 (f (2) - c * sinα); ED = c * cosα) 따라서 : AD = 제곱근 (f (2) - c * sinα) + c * cosα. 사다리꼴의.
4
과제 2. BC와 AD 직사각형을 찾아라. 사다리꼴의대각 BD = f의 길이가 알려져 있다면; 길이옆면 CD = c이고 그것과의 각도 ADC = α 해결책 : 사각 삼각형 CED를 고려하십시오. CE 및 ED면의 길이를 구하십시오. CE = CD * sin (ADC) = c * sinα; ED = CD * cos (ADC) = c * cosα.
5
ABCE 사각형을 고려하십시오. 직사각형의 속성에 의해 AB = CE = c * sinα. 직각 삼각형 ABD를 고려하자. 직각 삼각형의 특성에 따라 빗변의 사각형은 다리의 제곱의 합과 같습니다. 따라서, AD (2) = BD (2) - AB (2) = f (2) - c * sinα. 사다리꼴의 AD = 제곱근 (f (2) - c * sinα).
6
직사각형의 법칙에 의해 AE = AD - ED = 제곱근 (f (2) - c * sinα) - c * cosα. 사다리꼴의.
팁 5 : 사다리꼴의 작은 쪽을 찾는 방법
사다리꼴의 더 작은 기저부는 평행 한면 중 하나이며 최소 길이를 가지고 있습니다. 특정 데이터를 사용하여 여러 가지 방법으로이 값을 계산하십시오.
너는 필요할거야.
- - 계산기.
지침
1
두 가지 길이가 알려진 경우 - 큰 바닥사다리꼴 및 정중선 - 사다리꼴 특성을 사용하여 최소 기준을 계산합니다. 그에게 따르면, 사다리꼴의 중간 선은 기초의 절반 합과 동일합니다. 이 경우, 가장 작은베이스는 정중선의 두 배가 된 길이와이 그림의 큰베이스의 길이의 차이와 같습니다.
2
그런 사다리꼴 매개 변수를 아는 경우면적, 높이, 큰 바닥의 길이를 계산 한 다음 사다리꼴 수식을 기반으로이 그림의 최소 기준을 계산합니다. 이 경우, 최종 결과는 따옴표 붙은 이중 영역의 차이와 그러한 매개 변수의 높이를 사다리꼴의 큰 밑변의 길이로 빼서 얻어집니다.
3
직사각형의 가장 작은 변의 길이사다리꼴은 다른 방법으로 계산합니다. 이 매개 변수는 두 번째면의 길이와 그에 인접한 예각의 사인의 곱과 같습니다. 같은 경우 각도 값을 알 수없는 경우 사다리꼴 높이의 가장 작은 쪽면을 동일시하여 피타고라스 정리에 따라 계산합니다. 직사각형 사다리꼴의 가장 작은 변은 코사인 정리 (cosine theorem)를 사용하여 구할 수 있습니다. c² = a² + b²-2ab * cosα; 여기서 a, b, c는 삼각형의 변을 나타냅니다. α는 변 a와 변 b 사이의 각입니다.
팁 6 : 삼각형의 더 작은 높이를 찾는 법
삼각형에서 측면과 모서리 사이의 관계는 그림의 내부 선 (예 : 높이, 중앙값 및 이등분)과 연결되어 있습니다. 이러한 관계에 대한 지식은 문제의 해결을 크게 단순화시킵니다.

지침
1
삼각형의 세 가지 높이 중에서,이는 그림의 가장 큰 측면으로 낮아진다. 이것을 보시려면 삼각형의 세 가지 높이를 그 변의 크기를 통해 표현하고 비교하십시오. a면이 임의의 예각 삼각형의 세면 a, b, c 중에서 가장 크고,면 c가 가장 작다고 가정합니다. 측면 a에서 높이 h, 높이 b에서 측면 b, 높이 hc에서 측면 c까지를 나타냅니다. Height는 삼각형을 두 개의 직사각형 삼각형으로 나눕니다.이 삼각형은 항상이 높이가 다리 중 하나가됩니다.
2
높이의 헥타르는 a의 가장 큰면으로 그려지고,피타고라스 정리 (Pythagoras theorem)에 의해 결정될 수있다 : h² = b² - a1² 또는 h² = a2 - a2². 여기서 a1과 a2는 측면 a가 높이 ha로 나뉘어 진 선분입니다. 또한, 피타고라스의 정리에 따르면, 삼각형의 다른 두 높이를 그 변을 통해 표현하십시오 : hb ² = a²-b₁² 또는 hb² = c²-b²²; hc² = a²-c12 또는 hc² = b²-c²².
3
높이를 결정하는 공식 비교삼각형의 최대 측면 길이 - 공제 a₁과 같은 a₂ a₁² 및 ha² = s² 임 - a₂² - 삼각형, 상기 피감수 및 감수의 비율이 작은 점에서 차이 ha² = b²을주는 것이 명백하다.
4
삼각형의 더 작은 높이를 결정하기 위해 다음과 같이 할 수 있습니다.또한 삼각형의 알려진 각도의 사인을 통해. 조건이 코너의 대부분을 설정하면,이 각도는 가장 높은 손에있다, 그것은 가장 낮은 높이를 유지 정확하게 때문이다. 주어진 삼각형에 대한 상수 값 - 상기 대향 각도의 사인에 삼각형의 비율이 때문에 더 삼각형의 두 개의 다른 각도의 삼각 함수를 통해 원하는 높이를 표현 번거로운 계산을 방지한다. 따라서, 작은 삼각형 높이 HA = B * SinB 또는 하행 = C를 * B가 큰 쪽 (A)와 측면 B의 각도 싱크, 및 C - 높은 측 및 측면과 삼각형의 각도.